摘要：包括各种 DP 类型和优化技巧等。

wqs 二分

更应该说是一种思想吧。

我们希望知道恰好选择 $k$ 个物品时的答案，但世界上哪来的那么多恰好呢。令 $f_x$ 是恰好选择 $k$ 个物品时的答案，那么点集 $(x,f_x)$ 常会形成一个凸包，于是要知道特定 $x$ 的答案，就只需要二分出这个点的斜率，然后用截距加上横坐标乘斜率即可，这个过程就是 wqs 二分，而求最优截距的方法是多样的，下面会说。其中有许多需要注意的细节，比如连着几个值斜率相同（其实没关系，反正最后求出来的答案是一样的）。另外精度也是一个需要考虑的问题。一般用下面这种写法：

while(l<r){
	mid=(l+r>>1)+1;solve(mid);
	if(g[1].num>=n)ans=g[1].data+n*mid,l=mid;else r=mid-1;
	if(g[1].num==n)break;
}

最后出来的 $ans$ 就是我们想要的。其它的倒是没什么了，具体看题。

Akvizna link 忽略轮数的限制，用 $f_x$ 代表还剩 $x$ 个人的最大收益。于是有 $f_x=\max\limits_{i=0}^{x-1}(f_i+\frac{i-j}{i})$，可以拆成斜率优化的形式。推出柿子之后直接 wqs 二分即可，然后似乎要注意精度。

CF739E link 猜测答案在两个维度上都是凸包形式，所以可以二分套二分。检查的过程就变成了对于一个物品，用红球有 $p_A-c_A$ 的贡献，用蓝球有 $p_B-c_B$ 的贡献，两个都用有 $p_{A\&B}-c_A-c_B$ 的贡献，选择一个希望最大化总贡献，贪心即可，途中记录两种球各用几次。有些卡精度，应当在当前数量等于希望数量时及时推出。

aliens link 经典的题目。把右上的点翻到左下，消除那些对答案不产生影响的点，剩下的点会形成一个锯齿一样的形状，每个点映射到对角线上会有一个区间 $[l_i,r_i]$。但由于多次选择的区间只会被计算一次，所以方程会稍微复杂一点（一开始以为要多次计算，调了半天才反应过来，毕竟那种思路下根本无法形成凸包）。内部还是用的斜率优化。

忘情 link 和上一道题本质上差不多。柿子题。

林克卡特树 link 转化问题。把树拆成 $k$ 部分，然后要最大化连接起来后的答案，就贪心地选择每个部分中的直径。于是问题就变成了在树上选择 $k+1$ 条不相交的链。因为所以这玩意是上凸的，所以采用 wqs 二分。用 $f_{x,0/1/2}$ 代表这个点当前度数为多少时的最优值，考虑转移。用 $g_x$ 代表 $x$ 子树内的答案（也就是到父亲那条边不选），于是有

$\begin{aligned} f_{x,0}&=f_{x,0}+g_y\\ f_{x,1}&=\max(f_{x,1}+g_y,f_{x,0}+f_{y,1}+e)\\ f_{x,2}&=\max(f_{x,2}+g_x,f_{x,1}+f_{y,1}+e+p) \end{aligned}$

其中每个值都要记录两维，即答案和选择的链的数量。最后看 $g_{root}$ 选择了几条链并更新左右端点即可。

CF802O link 运用到了 wqs 二分思想的题目。因为所以它是一个凸包，然后就可以用 wqs 二分了。考虑内部如何检查，这里用到了反悔 DP 的思想。考虑一个点作为结束时间时选择谁作为开始时间。如果选择一个没有被选择过的 $a_y$，那么由于当前是一个新的决策，所以贡献是 $b_x+a_y-v$。如果是顶替掉之前的某个决策，那么贡献的变化值就是 $b_x-b_y$，所以动态维护 $a_y-v$ 和 $-b_y$ 的最小值并记录第一种决策做了多少次即可。一只 $\log$。

矩阵快速幂优化DP

一篇比较初步的方法总结。

矩阵快速幂优化递推最经典的应用是快速求斐波那契数列的某一项，由于过于简单在这里没有什么必要提。由此引申出一类和上面一样单纯地优化递推过程的题目。经典题目如 跳房子link，用 $f_x$ 代表跳到 $x$ 的方案数，用 $F_x$ 表示 $f$ 的前缀和，那么根据定义有 $f_x=F_{x-n-1}$，而 $F_x=F_{x-1}+f_x$，所以综合一下就是 $F_x=F_{x-1}+F_{x-n-1}$，于是就可以用矩阵快速幂来做了。转移矩阵是这样的：

$\begin{bmatrix} F_x\\F_{x-1}\\\dots\\F_{x-n} \end{bmatrix} = \begin{bmatrix} 1&0&\dots&1\\ 1&0&\dots&0\\ \dots&\dots&\dots&\dots\\ 0&\dots&1&0 \end{bmatrix} \times \begin{bmatrix} F_{x-1}\\F_{x-2}\\\dots\\F_{x-n-1} \end{bmatrix}$

然后就可以啦。由于 $\forall i\in[n+1],F_i=1$（显然是这样的），所以只需要计算转移矩阵的 $m-n-1$ 次方即可。答案是 $F_m$。中国象棋link 是相似的，用 $f_x$ 代表当前位置放了的合法方案，用 $g_x$ 代表当前位置没放的合法方案，于是有 $f_x=g_{x-1},g_x=f_{x-1}+g_{x-1}$。用 $t_x$ 代表二者之和，会发现 $t_x=2g_{x-1}+f_{x-1}=t_{x-1}+t_{x-2}$（傻逼才会这么慢慢推，没错我就是傻逼）。边界情况：$t_1=2,t_2=3$，矩阵快速幂去做即可。

另外一种比较常见的就是 AC 自动机上套用矩阵快速幂。P3041link 在 AC 自动机那篇文章中已经说过了，有另一道题也很不错。禁忌link 同样是在自动机上 DP，但是由于希望最大化串的价值，所以有贪心的想法是说一到串末就回到起点并统计答案，同时矩阵元素的意义应当是到达这一状态的概率（期望可加）。统计答案上有一个非常常用的技巧是说在矩阵中新开一个地方用于存储答案，对于可以贡献答案的位置 $x$ 赋值为 $a_{x,p}=P$，然后为了方便统计答案要搞一个 $a_{p,p}=1$，这样就可以在答案矩阵中直接找到答案了。

还有就是图上 DP，常见形式是什么求走了多少步之后能到达哪些点。CF576D 是比较朴素的那种，显然把时间分成一些阶段，对于每个阶段的末尾求出哪些点可以到达，然后剩下的路程考虑在当前边集的基础上广搜出最短路。这里有一个 bitset 优化乘积的方法，代码如下：

struct node{bitset<N>a[N];}newone;
inline node operator *(node x,node y){
	node an=newone;
	for(int i=1;i<=m;i++)for(int j=1;j<=m;j++)
		if(x.a[i][j])an.a[i]|=y.a[j];
	return an;
}

自然有许多变式，一种是常见的给边加权，一般而言权会比较小。此时就可以考虑拆边，把一个点拆成一串点，相邻的点有 $1$ 边，新点记为 $(x,p)$。连一条 $x$ 到 $y$ 权为 $w$ 的点可以转化成连一条 $(x,0)$ 到 $(y,w-1)$ 的边即可，然后就可以正常快速幂优化了。迷路link 是板子。WYC 差不多，不用多说。

轮廓线DP

模拟赛中遇到了，被迫花了一天来学习。

轮廓线 DP 本质上是逐格转移的状压 DP，有特别经典的图可以说明：

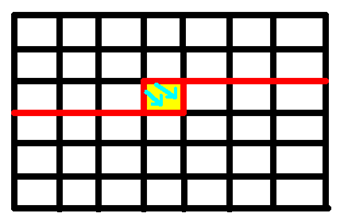
思想上非常好理解，就是把分界处的状态压缩起来。主要是实现上有许多技巧需要说一下。第一个是状态的表示方法，在大多数情况只需要用 0/1 来代表这个位置是否存在插头即可，一般会以二进制或者四进制的形式压缩成一个整型（$1$ 到 $n$ 位是对应和纵向插头，而第 $0$ 位放横向插头），操作的时候视情况展开成一个数组或者就直接对位进行操作。编码形式也比较重要，为了让状态确定唯一又尽量少，就需要采用一些优秀的编码形式。目前知道的有三种：无脑 $01$，适用于没有太多要求的场景；括号序列，适用于强制要求只有一个回路的场景；最小表示法，适用于希望选择一个连通块的场景。特别地，对于第三种，每次 insert 的时候都需要转化成最小表示法的形式（因为连通块之间是没有顺序的，所以可以多压一）。

然后是状态是转移方法，一般而言轮廓线 DP 每个阶段存在的合法状态不会特别多，所以可以考虑把合法状态哈希存储，然后在下一个阶段就只需要找出哈希表里所有的元素即可，发现这一部分是可以滚动的，进一步压缩空间（29009 是一把比较顺眼的钥匙）。对于一个状态，要转移到下一个阶段，就只需要提取出这个状态对应的上插头和左插头，然后加上自己的状态进行一大堆分类讨论就可以了。然后结合例题分析，毕竟剩下的东西因题而异。放个我的哈希板子：

struct node{int pl,data,nxt;};
struct Hash{
	node data[M];int nowCnt,head[H];
	inline void clear(){nowCnt=0;memset(head,0,sizeof(head));}
	inline void insert(int pl,int val){
		int key=pl%H;
		for(int i=head[key];i;i=data[i].nxt)if(data[i].pl==pl)return add(data[i].data,val);
		data[++nowCnt]=(node){pl,val,head[key]};head[key]=nowCnt;
	}
}h[2];

【模板】插头dp 插头 DP 的板子，由于强制要求只有一条闭合折线，所以需要用到括号表示法。特别的是由于希望覆盖满所有的格子，统计答案是时候只能在最后一个格子统计，并且此时强制上插头和左插头配对（这样才能做到不重不漏）。另外，如果当前格子恰好是两个左括号或者两个右括号时需要调转其中一个配对处的方向（调转上方显然好写，需要写个小小的函数来找到配对位置在哪）。然后就没了。

Eat the Trees 和上一道题很像，只是少了强制一条的限制，这样一来面对两个插头就不需要分类讨论左括号还是右括号了，所以状态的每一位只需要记录一个值即可。然后就不需要哈希了。

神秘的生物 最小表示法的应用，由于希望最后只有一个连通块，所以在上方有插头并且自己不选的时候要特别注意，如果自己不选会导致上插头断掉的话，那么这个状态就会是不合法的（判断上直接找轮廓线上有几个同类插头即可）。一个状态能贡献答案当且仅当轮廓线上只有一种插头（也就是当前只有一个连通块），然后就是要用最小表示法来缩减空间。

神奇游乐园 和板子是很像的，少了一些限制（每个格子不需要都选择，话说有了这个限制谁还搞 DP 啊），所以呢就多了一些决策，贡献答案的地方也就多了一些（要满足当前轮廓线恰好只有一对插头），然后就没什么了。

白金元首与莫斯科 也可以用状压来做。由于骨牌的结构是简单的，所以状态只需要记录一个布尔值即可，这样一来状态就非常稠密了，导致哈希大概率会被卡掉。转移上非常板。统计答案肯定不能每次暴力统计，考虑把这个点扣掉，那么当前点的答案就是从上往下到这个点的部分和从下往上到这个点的部分刚好可以拼起来并且不会延申到这个格子的方案，画图发现这等价于两个状态完全相同并且第 $0$ 位为假，枚举状态累加答案即可。

高维前缀和

又叫 SOSdp。一般而言可以使用高维前缀和来统计形如： $s_x=\sum\limits_{y\&x=y}a_y$ 的问题。代码上的形式如下：

for(int i=0;i<20;++i)
	for(int j=0;j<n;++i) 
        if((1<<i)&j) S[j]+=(S[j^(1<<i)]);

CF449D：考虑求有多少子集与起来不为 $0$。令 $num_x$ 为包含 $x$ 的数的数量（可以用高维前缀和求得），那么与的结果包含 $x$ 的方案数 $f_x=2^{num_x}-1$，于是使用子集反演可以求出有多少子集与起来不为 $0$，用总数减即可。复杂度 $O(N\log N)$。

P6442：相似地，令 $num_x$ 为 $x$ 包含的数的个数，那么结果被 $x$ 包含的方案也就是 $f_x=2^{num_x}-1$。然后反演可以求出有多少方案没有包含所有数，然后就可以得出答案了。

CF383E：一个东西不多说。