摘要:各种字符串算法。太难的以后再说。
后缀数组
板子部分:
后缀排序的中心思想是倍增,为了优化常数会使用一些比较特别的技巧。写法上主要分为两个部分,即预处理部分和倍增部分。首先定义几个数组, 是排名为 的数组的位置, 是后缀 的排名, 是第一关键字 的位置, 是按第二关键字排序后的数组(存的是原数组下标)。倍增部分也主要分为几步,先统计出 数组(尾巴上的肯定优先,剩下的按 序依次加入);然后统计 并填数,注意初始化;最后统计新一轮的 值(首先要把 的值复制到 中),最后在 退出。板子。
void main(){
int n=200,p=0;
for(int i=1;i<=m;i++)pl[rk[i]=w[i]]++;
for(int i=1;i<=n;i++)pl[i]+=pl[i-1];
for(int i=m;i;i--)sa[pl[rk[i]]--]=i;
for(int w=1;;w<<=1,n=p,p=0){
for(int i=m;i>m-w;i--)id[++p]=i;
for(int i=1;i<=m;i++)sa[i]>w&&(id[++p]=sa[i]-w);
memset(pl,0,sizeof(pl));
for(int i=1;i<=m;i++)pl[rk[id[i]]]++;
for(int i=1;i<=n;i++)pl[i]+=pl[i-1];
for(int i=m;i;i--)sa[pl[rk[id[i]]]--]=id[i];
memcpy(ork,rk,sizeof(int)*(m+1));p=0;
for(int i=1;i<=m;i++)rk[sa[i]]=chk(sa[i-1],sa[i],w)?p:++p;
if(p==m)break;
}
}
数组定义为后缀 和 的 长度。有结论是说 。所以有线性的代码:
for(int i=1,k=0;i<=m;i++){
if(k)k--;
while(w[i+k]==w[sa[rk[i]-1]+k])k++;
h[rk[i]]=k;
}
有许多结论。一个是说后缀 和后缀 的 值是 。另一个结论是一个串本质不同子串的数量,考虑添加每个后缀的前缀并去除掉重复部分,而重复部分就是之前的后缀中和它前缀相同的部分的交集,也就是求得的 ,所以本质不同的子串数量是 。
另外就是一个非常常见的柿子,给定一个集合 ,求 。发现问题可以变成 ,然后把这玩意提取出来就可以用单调栈来快速处理了。
再有就是练习题时间了。
优秀的拆分:首先枚举贡献点,然后把问题拆分成以一个点开头的 串数量乘上以那个点结尾的数量。然后考虑枚举 部分的长度,每隔 个点设置一个关键点,可以想到一个合法的 串会恰好包含两个关键点。一对相邻的关键点分别向两个方向求出最长公共前后缀,最后会得到这样一张关键的图:
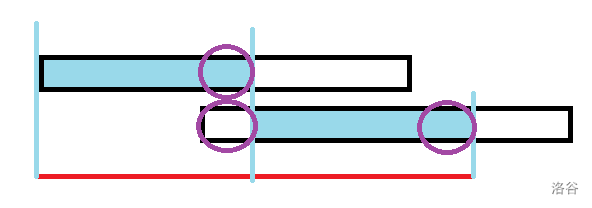
关键点并没有画出来。黑色的串是最长的相同前后缀拼起来形成的串,红色的是一个长度为 的串。会发现紫色部分是相同的,所以红色的串一定是合法的。也就是说最右边的空白中的点都是可以作为右端点的,差分实现即可。然后调了两个小时,这启示我在开始敲键盘之前一定要把各种细节就先想好,否则会在一些地方纠结很久并浪费很多时间。
CF822E 首先有一个贪心的想法,当确定了用 的一个前缀去匹配 ,并且使用的次数是固定的情况下肯定是越往后匹配越优。所以用 代表 的 前缀使用 次机会最多能匹配到 的最长前缀的长度,然后考虑这个状态能转移到哪些。 不用说,令 是 的 后缀和 的 后缀的最长公共前缀,那么这个状态也可以贪心地转移到 ,过程中统计是否有合法状态即可。求公共前缀可以考虑把 和 拼起来(中间加一个分割符号),然后把问题转化成求新后缀的公共前缀即可。
品酒大会 提出了一个常用的做法。两个后缀的 不小于 当且仅当他们之间的元素都不小于 ,也就是说把所有 对应的位置 合并之后呢二者在同一个集合内,所以可以用并查集来实现。具体到这道题就只需要离线下来,按 降序排序之后呢合并,维护每个集合的最大次大最小次小以及集合的 ,这些就非常套路了。
后缀自动机
以下内容为初学笔记,非常幼稚。
有一个串 aabab,对它的所有后缀建立字典树,会得到:
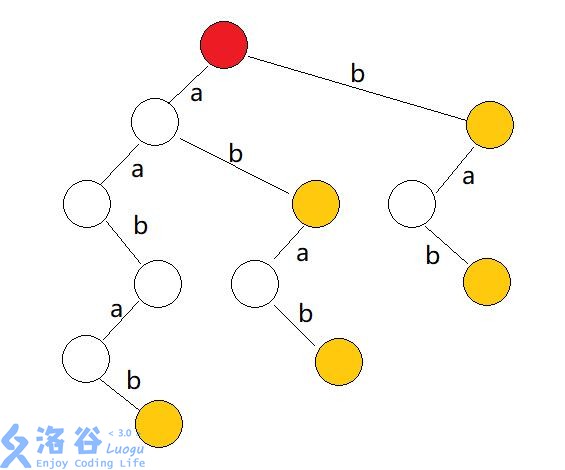
点太多了,不是非常优秀,而且复杂度太高了。所以想着能不能用一些什么方法把复杂度和点数降下来,这就是后缀自动机想要做的事。先搞一个定义,一个串的 简称() 是指的这个串在原串中出现位置(指结尾位置)集合。于是就有了一些结论:
- 若 ,那么 是 的后缀(或者相反)。
- 对于两个串 ,有 ,要么 。
- 所有 相同的 称为一个等价类,一个等价类中串的长度连续。
根据第一个和第二个结论,所有等价类可以形成一个树形结构,事实上 SAM 就是把这棵树上的节点重新编号连边后形成的东西。比如串 aababa 的这棵树(即 ,下面叫 )是这样的:
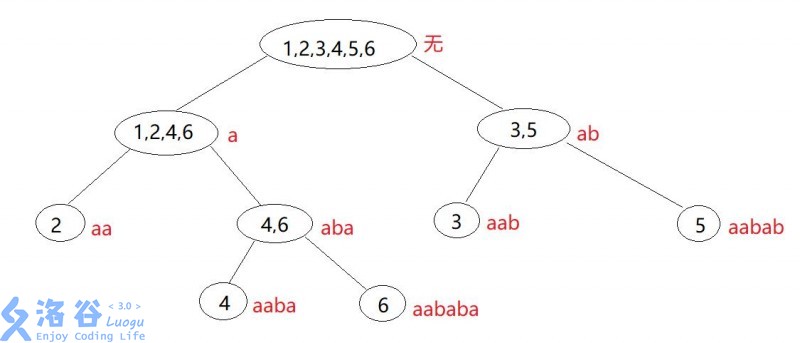
- 记 是等价类 中最短的字符串长度,而 是最长的,那么有结论: 是 的父亲当且仅当 。
性质就差不多了,还有一些正确性和复杂度上的证明然鹅我并不很想研究。于是就是最重要的构造部分了,放个非常经典的图。
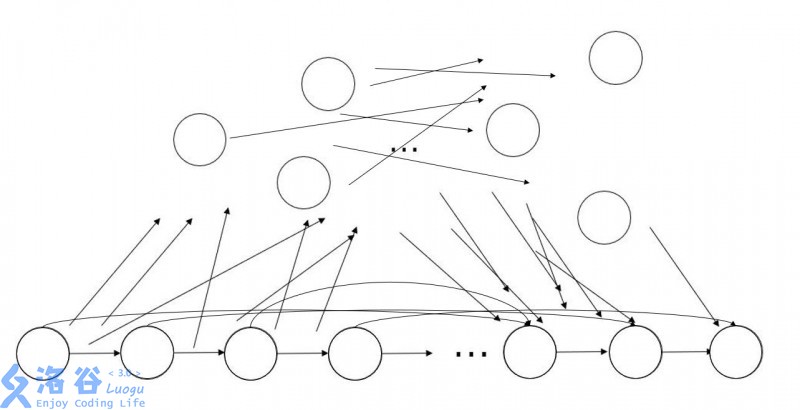
主程序非常无脑,一个一个字符加,构成了最下面那排节点。
for(int i=1;i<=m;i++)insert(w[i]-'a');
首先是新建一个节点(毕竟新串的 不属于任何其它等价类),有:
int p=lastCnt;int np=lastCnt=++cnt;
t[np].len=t[p].len+1;
然后开始遍历加入该字符之前的串的后缀并检查哪些位置的 会变。有:
for(;p&&!t[p].ch[c];p=t[p].fa)t[p].nxt[c]=np;
if(!p)t[np].fa=1;else{}
如果进到了第二个分支就说明 在原串中出现过,那么由于这个点到根的所有点都是自己的后缀,那么这条路上的所有点的 集合大小都应该加一。所以呢就可以考虑直接把这个点和新的点建立联系,如下:
int q=t[p].ch[c];
if(t[q].len==t[p].len+1)t[np].fa=q;else{}
还有其它情况,若 怎么办。这个情况等价于 ,也就是说有一个比 更长的串属于 ,而这个东西一定不是新串的后缀,因为如果是的话那么去掉 之后一定是旧串的后缀,既然长度更长那么应该先被跳到。所以,属于 的长度不大于 的串是新串的后缀,但大于的却不是,所以 对应的集合就无法放在同一个圈内而需要拆分了,这就是上方杂乱节点的由来。
新建一个叫做 的节点,用于存放那些 中多了一个元素 的串。然后考虑它的出边, 以及 。显然 ,由上面第二类情况的分析可知。出边和 方面,会发现其实和原节点的差不多的,所以可以直接整体赋值。然后由于这玩意的 比别人恰好多了一个 ,所以它就能当 和 的父亲啦。写出来是这样的:
int nq=++cnt;t[nq]=t[q];
t[nq].len=t[p].len+1;
t[q].fa=t[np].fa=nq;
最后就是和上面第二部分一样的套路,更新一路上的出边。
for(;p&&t[p].ch[c]==q;p=t[p].fa)t[p].nxt[c]=nq;
总的就是这样的:
inline void insert(int c){
int p=lastCnt;int np=lastCnt=++cnt;f[np]=1;
t[np].len=t[p].len+1;
for(;p&&t[p].nxt[c]==0;p=t[p].fa)t[p].nxt[c]=np;
if(!p)return t[np].fa=1,void();
int q=t[p].nxt[c];
if(t[q].len==t[p].len+1)return t[np].fa=q,void();
int nq=++cnt;t[nq]=t[q];
t[nq].len=t[p].len+1,t[np].fa=t[q].fa=nq;
for(;p&&t[p].nxt[c]==q;p=t[p].fa)t[p].nxt[c]=nq;
}
用自然语言描述这一过程就是说,进来一个字符,更新一串点的出边;如果到头了就返回,否则检查一下是否有合适的父亲。如果有,回去;如果没有,说明有个集合太霸道,从中扯出来一部分,并钦定它是父亲,然后打扮一下这个节点,走完流程,更新出边。好感性的语言啊。
复杂度什么的,由于 ZC 没有脑子,自然是没有那个能力去看的,暂且略过罢。先看一下应用部分。其实吧后缀自动机大多数的应用都来源于它最底层的性质:从根随机游走,任意合法的路径(结束节点没有任何限制)都是原串的子串,并且不重不漏,这个性质听起来就已经非常美妙啦。然后点呢有一些实际含义,比如每个节点的 代表这个集合中最长的子串的长度,然后上面代码中的 是每个节点对应的 集合的大小。
- 判断子串
在自动机上顺着边跑,如果跑到 了就说明不是,否则是。
- 不同子串的个数
后缀数组上直接用总串数减去 即可。后缀自动机上考虑 DP,用 代表从 出发的子串个数,由于 SAM 上任意从原点出发、并在任意点结尾的串都是原串的子串并且不会重复,所以用 ,然后 就是答案。
- 求子串不去重字典序第 大
首先预处理出每个节点 集合的大小。对于在串中第一次出现的点(即 ),直接令 即可。然后进行一次 DP,方程是 。
然后用 代表从 出发不去重的子串个数,有 ,所以找第 大就只需要贪心地找下去,按字典序遍历儿子,如果当前儿子少了就下一个,否则就进入到这个儿子当中,然后就可以啦。
还有很多很多方法和技巧,以后遇到了再说。
kmp 自动机
以 P3193 为例来说一下。
令 代表前缀 后面接一个字符 的字符串后缀和原串的匹配情况。显然有:
回到这道题,可以用 表示现在已经匹配到 ,加一个字符能变成匹配到 ,这个字符的方案数。显然有:
令 表示已经写了 个字符,目前已经匹配到 的方案数。枚举上一个位置已经匹配到了哪里,有:
然后就可以用矩阵快速幂来优化转移过程了。
稍微注意一下,在我的写法中,由于采用的是单列的矩阵,故而转移矩阵是这样的:
即转移矩阵是反直觉的,赋值的时候要注意一点。
AC 自动机
AC 自动机是更高维的 kmp。构造方法感觉更像是运用了 dp 的思想,先对所有模式串建立一棵 Trie 树,然后考虑某个节点 ,有个 的后缀,考虑如何去求它的 fail 值。于是就有了 AC 自动机的核心代码:
int x=q.front(),ff=t[x].fail;q.pop();
for(int i=0;i<26;i++)
if(t[x].nxt[i])t[t[x].nxt[i]].fail=t[ff].nxt[i],q.push(t[x].nxt[i]);
else t[x].nxt[i]=t[ff].nxt[i];
单纯匹配的题有 第一块板子。
比较无脑的就是可以在 AC 自动机上 DP,和在 kmp 自动机上 DP 是同一个道理。P4052 是板子,套路是以当前匹配到的位置 作为状态进行转移,决策就是下一个字符放啥,然后正常转移即可,在这道题中的限制就是不能转移到有 end 的节点,把这些点忽略即可。显然它是可以用矩阵来描画的,P3041 是矩阵快速幂优化 DP 套 AC 自动机,缝合题。P7456 不能算是 AC 自动机上 DP,而只能算是帮助 DP,不知道应该归到哪里。
一般的题目都会用到 fail 树的性质。自动机上每个点往 fail 对应的点上连边,显然最后会形成一棵树(每个点只会往更浅的点连接)。有一个显然的性质是,对于一个节点 ,它到根的路径可以看成是 kmp 的一个匹配过程,所以实际上这些点的串都是 串的后缀,这就非常有用了。在 第二块板子 中,我们现在停留在 ,那么实际上达到的效果是点到根所有点对应的串都出现了一次,然而暴力去找显然是不行的。于是可以找每个点出现的次数,然后回答的时候可以看成是一次子树求和(因为子树内的值会对它产生贡献)。P3966 也是一个意思。
fail 树也是树,所以可以树剖,这牵扯到一个性质。首先根据字典树的原理,一个节点在字典树上到根的所有节点形成了它的前缀集合,而一个串在另一个中出现可以看成前者是后者前缀的后缀。而前面也说了, 是 后缀表现为在 fail 树上 是 子树中的节点,所以要统计一个串在另一个串中出现了几次,就只需要把后者到根(字典树上)的所有点标记一下,然后查找前者子树中有多少个标记节点即可,用树状数组可以维护。P2414 就是这个方法,一个结论是说对于题目中所言的过程,虽然串的总长度可能很大,但建出来的 Trie 树不会太大(甚至可以边输入边建树)。把所有 离线下来排序之后按顺序回答就可以保证修改的次数是线性的,这样一来就可以用上面那种方法了,复杂度有一只 log。CF163E 会更简单一些,当前匹配到的点的贡献是 fail 树上点到根的权值之和,所以说修改操作就是单点修改,询问就是链查询,转化成子树修改单点查询即可,树状数组维护,一只 log。
